What are your existing beliefs and assumptions about this area of mathematics?

• Should we encourage pupils to develop quick recall of mathematical facts?
• Does understanding of mathematical procedures matter? Or is accurate use of these procedures more important?
• Is it better for pupils to have a single strategy for solving a problem, or a choice of multiple different strategies?

If all teachers of mathematics in your school were asked these questions, would there be broad agreement in their answers?

Mathematics is a fascinating and complex discipline. While expert mathematicians see the subject as a rich tapestry of interconnected ideas and concepts, there is a danger that novice learners can see it as a series of discrete and distinct ideas existing in silos.

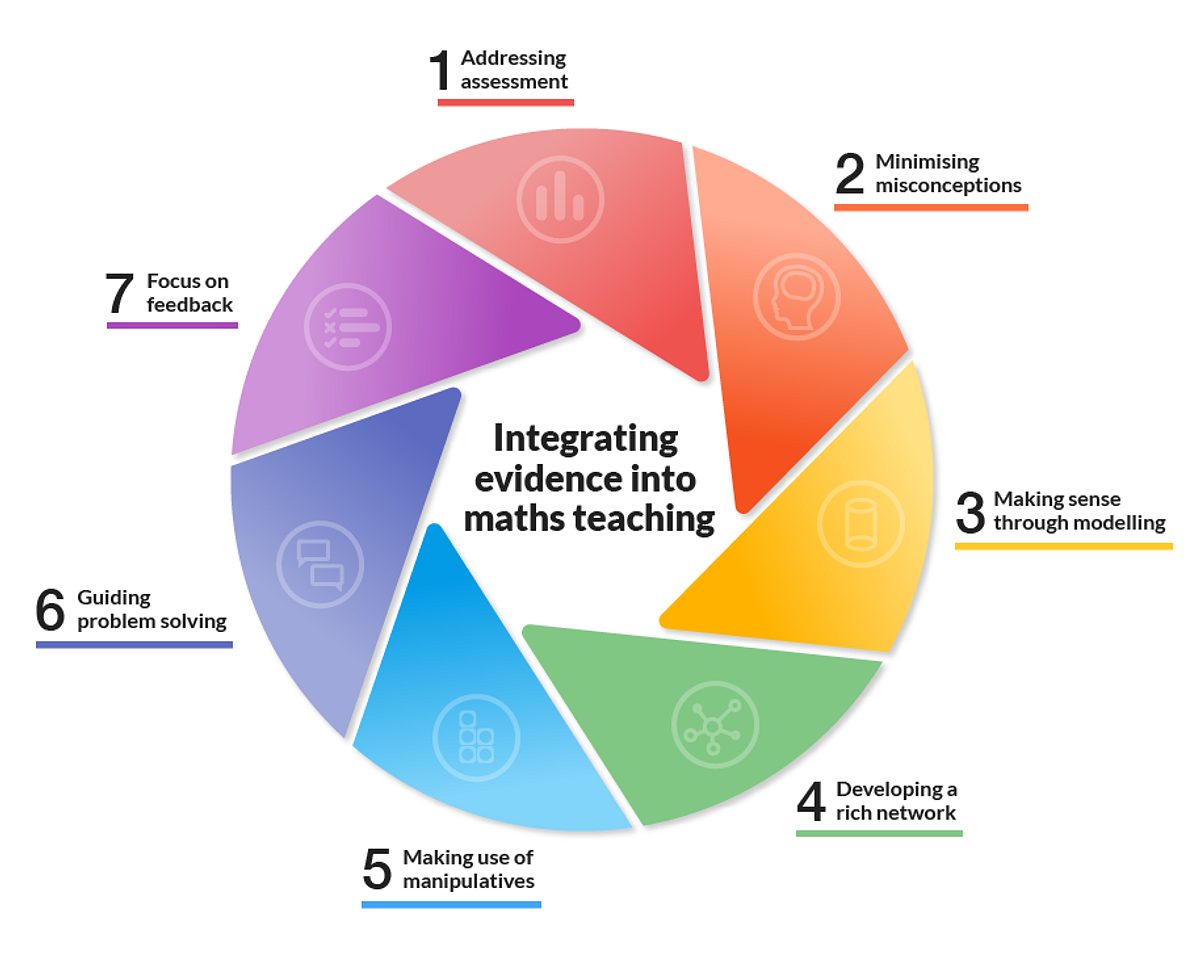
Given that joining these ideas together is essential to a full understanding of the subject, it is useful to consider the evidence around how we might develop this in our learners. Our guidance report, based on an extensive review of the evidence on teaching KS2 and 3 mathematics, found that:

• Teachers should emphasise the many connections between mathematics facts, procedures, and concepts.
• We should aim for pupils to develop quick, fluent retrieval of number facts.
• While fluent recall of procedures is important, teachers should also ensure that appropriate time is spent on developing understanding of these procedures.

• Pupils should be taught different methods and strategies for solving problems, and encouraged to think about when different methods are appropriate and efficient.
• We should build on pupils’ informal understanding of multiplicative reasoning to introduce procedures.
• Teachers should teach pupils that fractions and decimals extend the number system beyond whole numbers – number lines are a useful tool for teaching these concepts.

So, what might this look like in the classroom?

Addition of fractions

Pupils often struggle with fractions. It isn’t hard to see why: fractions don’t follow the intuitive rules for addition and subtraction, fractions which at a glance appear to be entirely different are actually equivalent, and the importance of fractions isn’t immediately obvious outside of their use in sharing problems.

For these reasons, it is often tempting to fall back on the use of procedures for manipulating fractions – such as the one featured in our first vignette. But this can be counterproductive, with evidence supporting the view that use of procedures without an underlying understanding of how and why these procedures work could be storing up problems for further on in the learning journey. This is because pupils can easily forget steps in the procedure – or forget the procedure entirely – and only an understanding of the mathematical mechanisms can support them in filling in these gaps.

As an example, consider the calculation below:

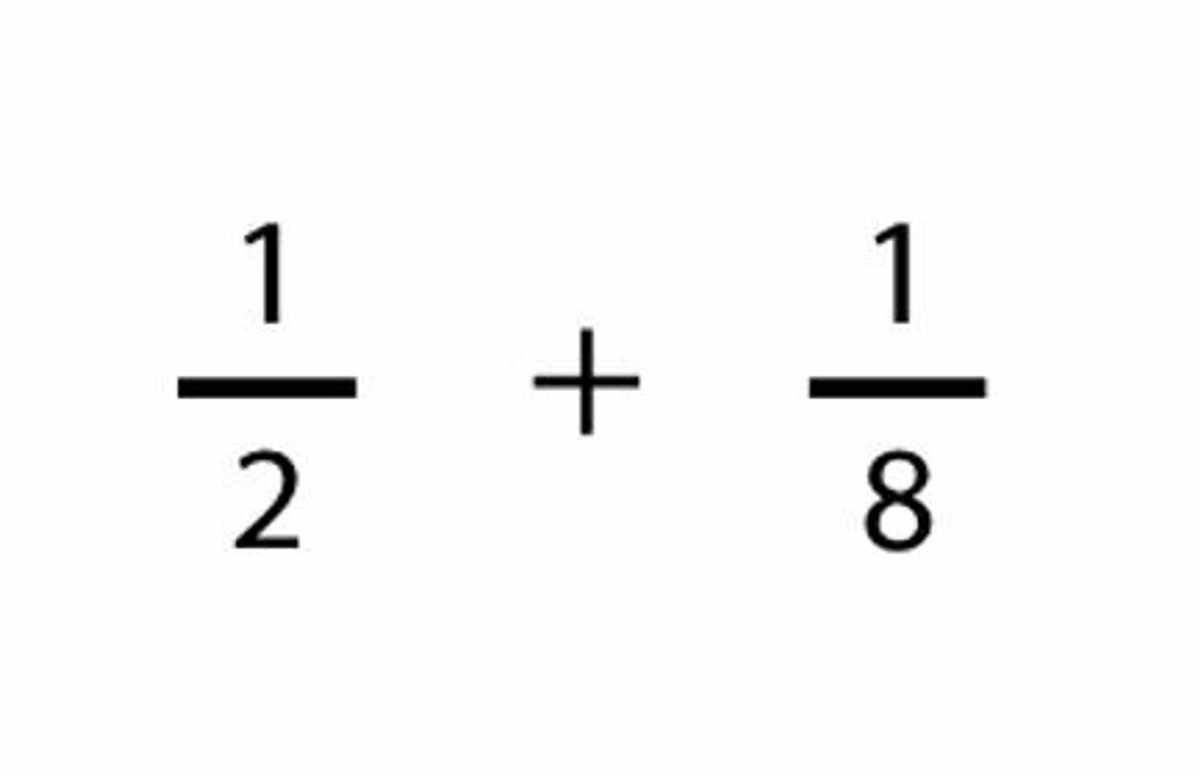
It is clear and obvious why a pupil might think the answer is two tenths. This answer makes sense as a misconception as it extends the rules of addition beyond their usefulness.

There are procedures to tackle this, an example of which features in our vignette. These procedures work, and a pupil might initially seem to be grasping addition of fractions by using them. But without an underlying mathematical understanding, what happens when the procedure is forgotten? Well it’s likely the pupil will reach once more for the rules of addition, and the familiar answer of two tenths will rear its head again.

An alternative approach

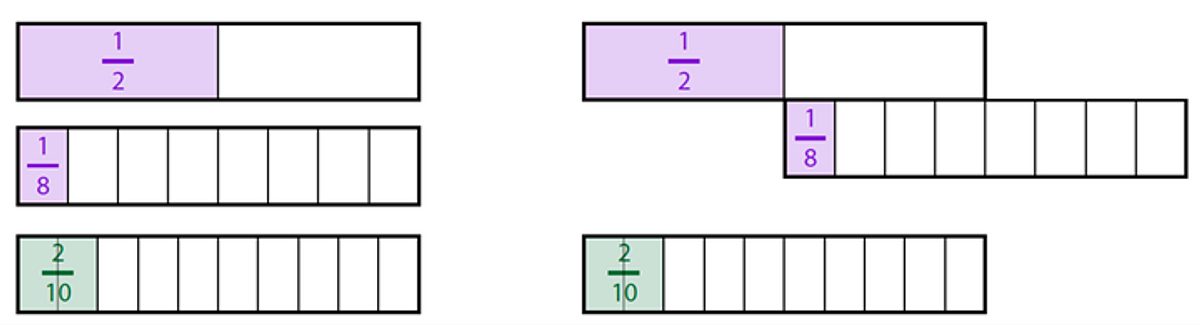
By considering fractions as extensions of the number system beyond whole numbers, and by encouraging the use of number lines and bar models, we can develop over time an understanding of the structure beneath the procedure.

Bar model

Number Line

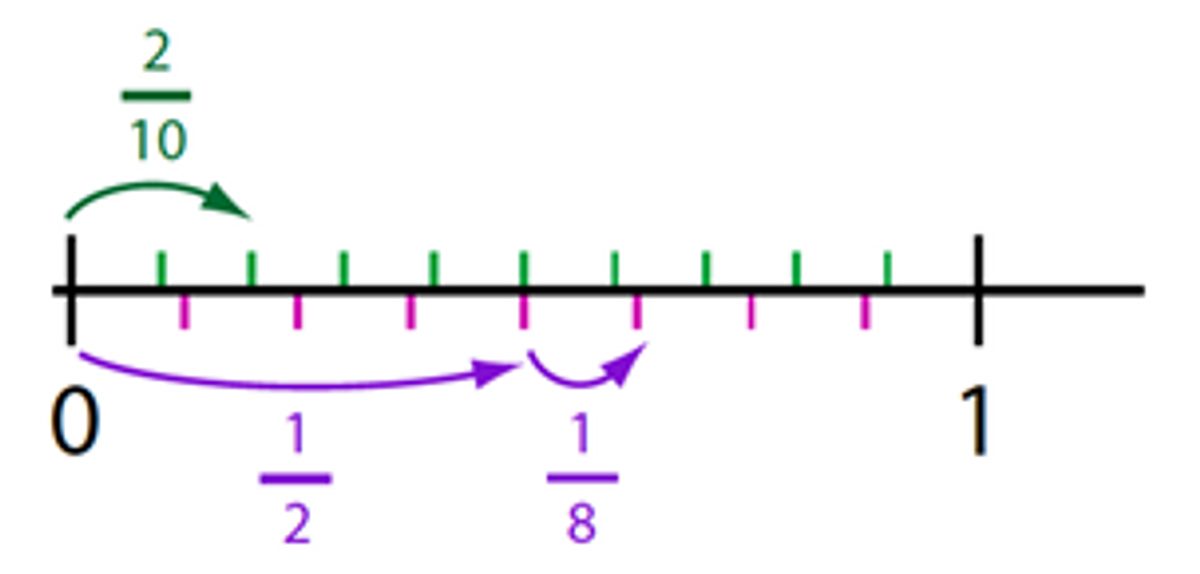
While pupils may then go on to use procedures – in much the same way as I do – this understanding is likely to support them should the procedure be either partially, or completely, forgotten.

‘Big questions’ for discussion

• Is time given to ensure that pupils develop understanding of the mathematical procedures they use in lessons, alongside fluent recall of these procedures?
• Do teachers take time to deliberately and explicitly emphasise the many connections between mathematical facts, procedures and concepts?
• Is explicit attention given to teach pupils that fractions and decimals extend the number system beyond whole numbers?