The phrases ‘All, some and none’ and ‘it must be, it can’t be, it could be’ may appear simple, but they are an indispensable part of my teaching practice.
According to Gaunt and Stott (2019), sentence stems like these are the ‘simplest and most effective technique for scaffolding talk’. But what exactly are they, and why should we use them to help develop high quality talk in the maths classroom?
Sentence stems scaffold pupils’ talk by supporting them to start a sentence. This enables pupils to concentrate on what to say rather than how to say it.
EEF’s‘Improving Mathematics in Key Stages 2 and 3’ guidance report highlights how ‘discussion and dialogue can be useful tools for developing metacognition, but pupils may need to be taught how to engage in discussion’.
The TOLD framework provides four key principles for promoting high-quality talk in maths:
Take part
Opportunities
Links
Debate
The use of sentence stems is one way that we can support pupils to ‘Take Part’, by providing scaffolding to prompt and extend their thinking.

Sentence stems can encourage pupils to engage in ‘exploratory talk’, in which they discuss, express contrasting views and opinions in a respectful way, whilst also explaining their reasoning.
Let’s consider these examples from the DfE (2020) Maths Guidance.
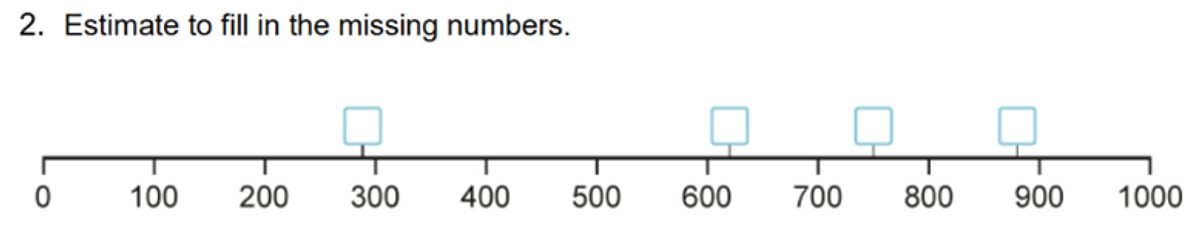
Framing how children can explain their reasoning, providing them with the sentence stems, ‘it must be, it can’t be, it could be’ helps scaffold high-quality talk and debate.
For example, when asked to estimate the first missing number in the example above, pupils in my class responded with:
“It must be a number between 200 and 300 but a value that is nearer to 300.”
“It can’t be a number less than 250 because the point is after halfway between 200 and 300.”
“It could be 290 because 290 is greater than 250 but less than 300.”
The sentence stems enable pupils to create ‘links’ and build upon each other’s ideas in order to extend their thinking.
We also know the importance of creating ‘opportunities’. This links to recommendation 2 of the‘Improving Mathematics in the Early Years and Key Stage 1 guidance report, and can also provide rich opportunities to support pupils’ understanding of mathematical structure (recommendation 4 of the Improving Mathematics in Key Stages 2 and 3 guidance report).
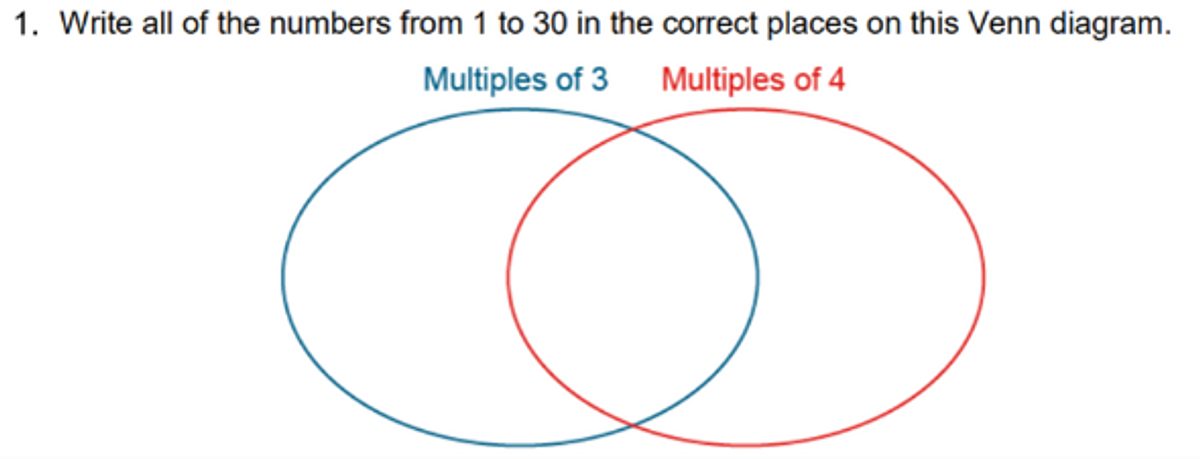
Using open questions such as, ‘What’s the same, what’s different?’ and then scaffolding pupils’ responses using the sentence stems ‘all, some and none’ can support pupils to uncover mathematical structure.
When I used this activity with my class, responses included:
“All multiples of 3 and 4 are even numbers as the products have a ones digit which is even e.g. 0, 2, 4, 6 or 8”.
“Some multiples of 3 are even and some are odd.”
“None (No) multiples of 4 are odd because the products never end in 1, 3, 5, 7 or 9.”
By scaffolding pupils’ talk using this set of sentence stems, I could assess pupils’ fluency, but crucially, it also provided an opportunity for pupils to demonstrate their understanding and reasoning, by elaborating and building on their own ideas as well as those of others.
Sentence stems like these have become one of the strategies I use to promote high-quality exploratory talk. They scaffold the ability to articulate reasoning, equipping pupils to think and talk like mathematicians.
References
DfE (2020) Mathematics Guidance: Key Stages 1 and 2 Non-statutory Guidance for the National Curriculum in England.
Gaunt, A., & Stott, A. (2018) Transform teaching and learning through talk: the oracy imperative. Rowman & Littlefield.
Mercer, N., Wegerif, R., & Dawes, L. (1999) Children’s talk and the development of reasoning in the classroom. British Educational Research Journal, 25(1), pp. 95 – 111.
