Education Endowment Foundation:EEF blog: Using worked examples to support mathematical problem-solving

‘Dad is making sandwiches for a party. He has 3 types of bread, and 5 fillings. Each sandwich has only one type of bread and one filling. How many different sandwich combinations can he make?’

When faced with mathematical problems such as this, many pupils struggle to think flexibly or to combine and apply prior learning in a new context. Pupils may not know where to start and can often resort to guesswork when their way ahead appears unclear.

Colin Foster¹ reflects that, with problem-solving, ​“the lesson begins when the problem is solved”. This means that one of the richest opportunities for learning about problem-solving lies in the reflections which take place after a solution has been found.

Reflecting upon completed problems enables learners to consider the choices which have been made and – crucially – the rationale underpinning these. This means focusing in on what we do during problem-solving, and why we do this.

One of the ways we can do this is by using worked examples. Recommendation 3 of the EEF’s ​‘Improving Mathematics at Key Stages 2 and 3’ guidance report highlights the role of worked examples in enabling pupils to analyse the use of different problem-solving strategies.

Worked examples present the problem and solution together. This reduces pupils’ cognitive load when they consider a questions, removing the need for them to carry out the procedures required to reach the solution. Instead, they are supported to focus on the reasoning and strategies involved.

For example, there are often various ways to approach a problem. Providing pupils opportunities to explore these different strategies in more detail – to identify similarities and differences, to unpick the approaches used and consider why they have been selected – can provide a powerful opportunity to develop mathematical understanding, as well as metacognition. This also allows discussion of the advantages and challenges of different choices, supporting pupils to critically evaluate these, using the knowledge gained to inform their future actions.

Evidence from the IES What Works Clearinghouse ​‘Improving Mathematical Problem Solving in Grades 4 Through 8’² tells us that through providing regular opportunities for pupils to examine multiple different strategies, they can become more confident, efficient and flexible in selecting appropriate approaches.

For instance, the worked examples below present two different strategies for organising recording when finding all possible solutions to a problem. Whilst these are not the only two possible ways to organise recording, presenting multiple different approaches via completed worked examples allows pupils to evaluate those problem-solving strategies, which in turn supports their understanding.

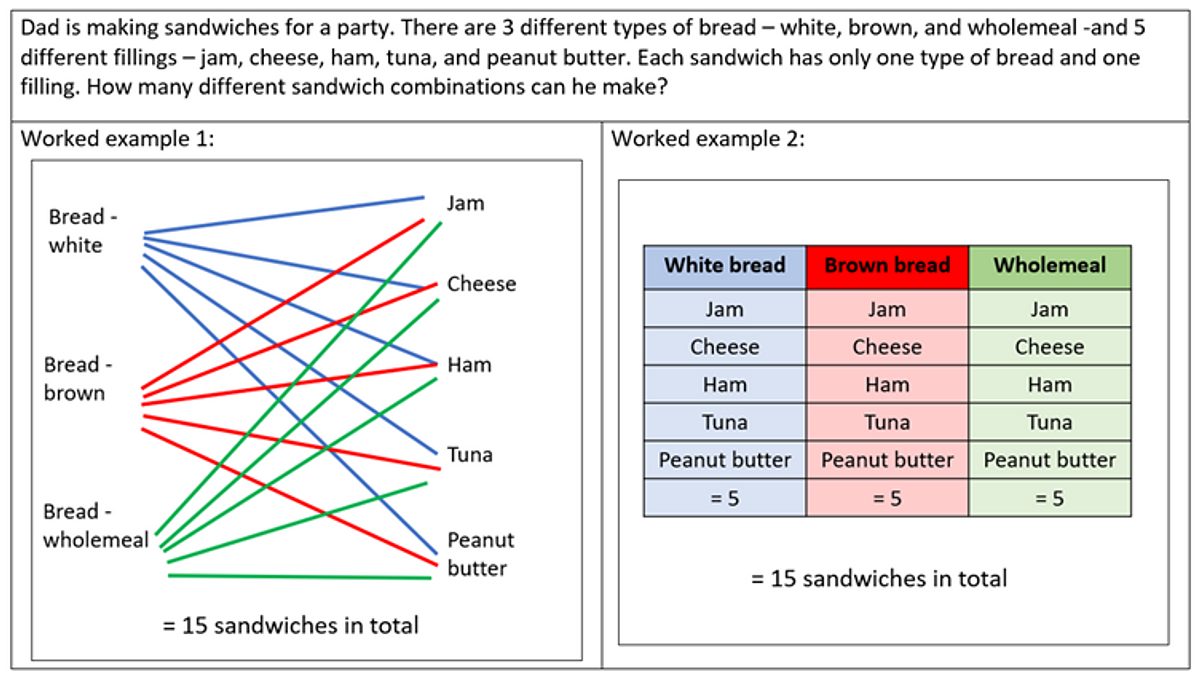
Using worked examples in this way allows us, as the teacher, to unpick any common errors or misconceptions. It also enables us to use these worked examples as a starting point for further discussion about alternative possible ways of working and to critically evaluate these, including by considering efficiency, helping to educate pupils about the range of possible options which are open to them in problem-solving.

Analysing and discussing worked examples helps pupils develop a deeper understanding of the processes used in problem-solving, and also supports pupils to reflect upon and communicate this reasoning. This means that, when exploring worked examples, the questions that we ask are key.

We can support and encourage pupils to reflect on the strategies and approaches featured in the worked examples through ​‘debrief’ questions, which consider the success of the strategies used, how these could be used more effectively, and support pupils to identify other scenarios in which these could be useful. Many of the questions we can use at this time aim to explore the​‘what’ and the​‘why’ of the strategies employed in the worked examples:

• Which strategies have been used here? Why?
• What worked well? Why?
• What was challenging? Why?
• Is there a better way to…?
• When else might you use…?
• What changes would you make to…? Why?

Working in this way provides opportunities for pupils to really delve deeper in their thinking about problem-solving, focusing less on the specific steps which may be needed to solve a single, unique problem, towards more critical – and ultimately useful – reflections about how problem-solving works.

Worked examples – by encouraging pupils to compare and analyse different strategies and approaches – provide another extremely valuable means of making those invisible processes of thinking and learning visible, demystifying these so that pupils can see first-hand what successful problem-solving looks like.