- Evidence consistently shows that educators can implement approaches that benefit young children’s mathematical skills and knowledge. The EEF’s Early Years Toolkit estimates that effective early numeracy approaches typically increase children’s learning by about seven months.
- Using multiple approaches together could aid children’s mathematical development. Facilitating mathematical language underpins other approaches.
- To support effective maths teaching, educators need to know how children’s maths skills develop, how to teach maths (pedagogy), and have knowledge of maths itself. The Evidence Store focuses on approaches for teaching. This overview page briefly introduces how children’s maths skills develop.
- While there is evidence that implementing these approaches could have a positive impact on children’s maths outcomes, there are still some questions that are unanswered and so more research is needed.
Mathematics plays a key role in a child’s development. Very young children are naturally curious, noticing differences in quantity and the shape of objects. They use early mathematical concepts when they play. Mathematical understanding helps children make sense of the world around them, interpret situations, and solve problems in everyday life. This could be talking about objects, sharing amounts with their peers, or counting in play. Developing a sound understanding of maths when we are young is essential. If children have a good early mathematical understanding they are more likely to do better later in school. It is also connected to their educational progress, and life outcomes.
How do children’s maths skills develop?
Mathematical development involves acquiring skills, understanding concepts, and gaining factual knowledge across a range of topic areas. These include topics such as quantity and number, operations, shape, and space. It also involves forming connections between concepts. An example is connecting the numeral ‘3’ with three objects. Children also need to develop reasoning skills such as logical thinking and the ability to predict and communicate their ideas.
A large amount of research on how children learn maths has revealed how complex it is. The rate of mathematical development relies on specific mathematical knowledge and other skills. These include:
- executive functions – such as working memoryWorking memory is an executive function that describes our ability to temporarily hold and manipulate information in our mind. It acts like a mental notepad that helps us complete tasks and solve problems., which is the ability to hold information in your mind and manipulate it;
- language and motor skills;
- children’s prior mathematical experiences; and
- children’s interests, enjoyment, and attitudes towards maths.
Developing a secure grasp of early mathematical ideas takes time. Even if a child appears to be engaging successfully in mathematical activities they may not have a full grasp of the underlying concepts. For example, they might be able to say the count sequence correctly but not understand the meaning of numbers within it. Children may also appear to have grasped an idea in one context but then not show that knowledge in a different context. There are different possible paths that children may follow in developing an understanding of a mathematical topic. ‘Developmental progressions’ are descriptions of the usual path that children follow in developing such an understanding.
Mathematical developmental progressions
The spirals below are examples of how children’s maths develops in different topics. They highlight how individual skills or concepts develop over time. While there is generally an order in which these skills may emerge, development does not take place in clearly defined linear steps. Some children may develop several skills at the same time. Other children may learn skills in different orders. This is why the diagrams are a spiral. To reach full understanding, children will need to master each of these skills. While each spiral is a separate diagram, there is considerable overlap across the topics.
Understanding how mathematical concepts typically progress can help educators understand what children need to learn next. It also helps them to build on what children already know. Then educators can expose children to a range of experiences so they can gain a full understanding of mathematical topics.
These spirals come from the EEF’s Improving Mathematics in the Early Years and Key Stage 1 guidance report. The research and recommendations in that report go beyond early years teaching. Educators should carefully consider the age of the children they are working with when planning what content to cover.
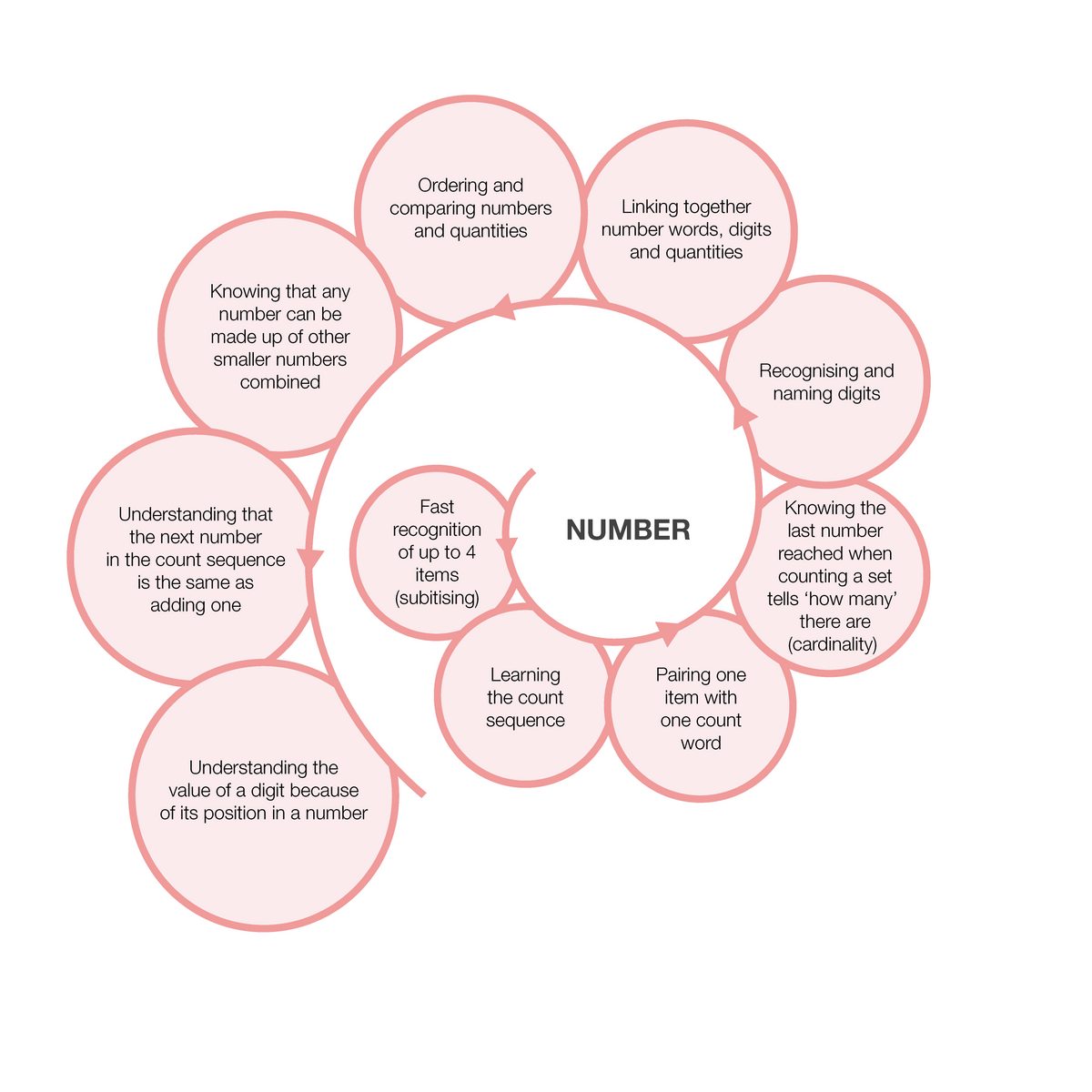
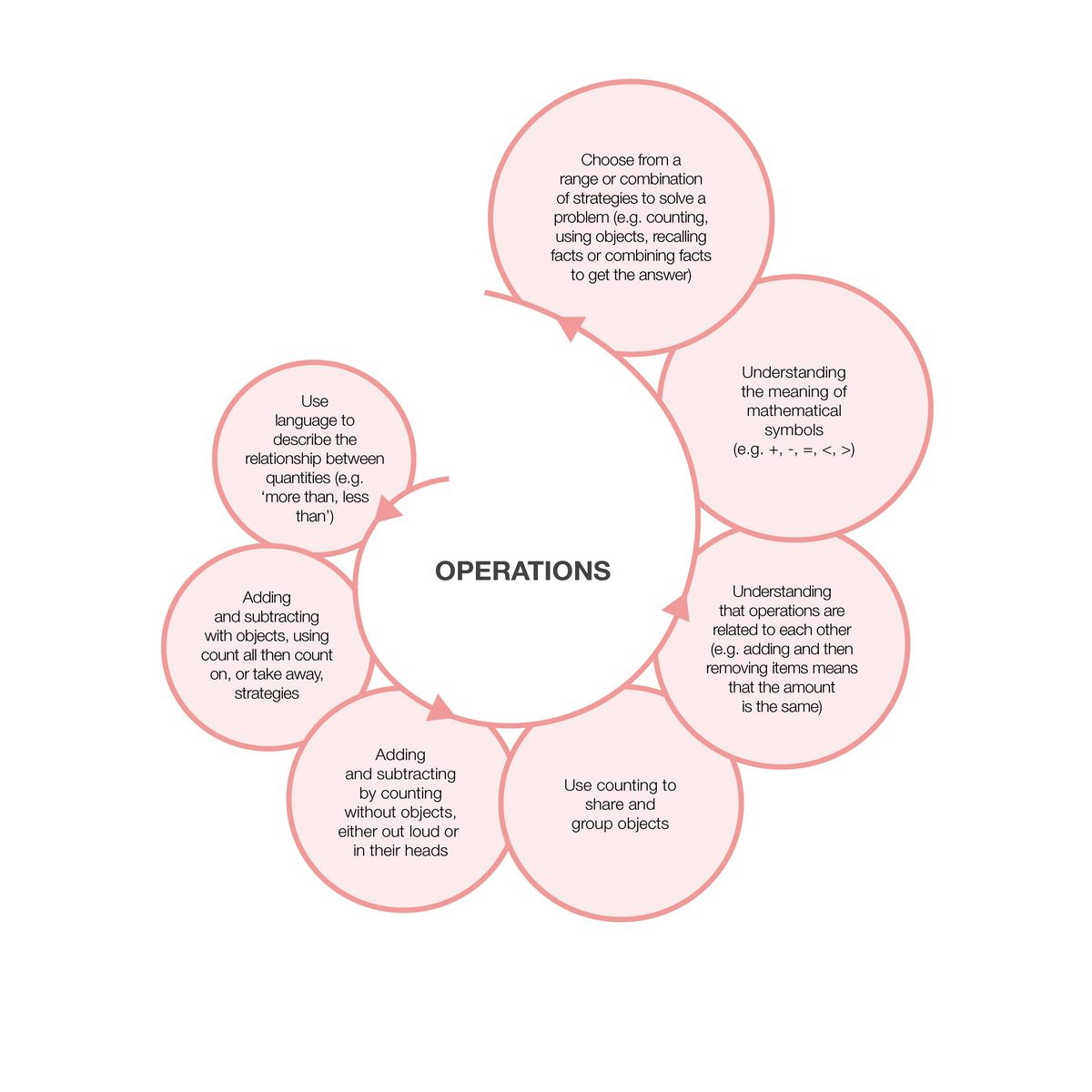
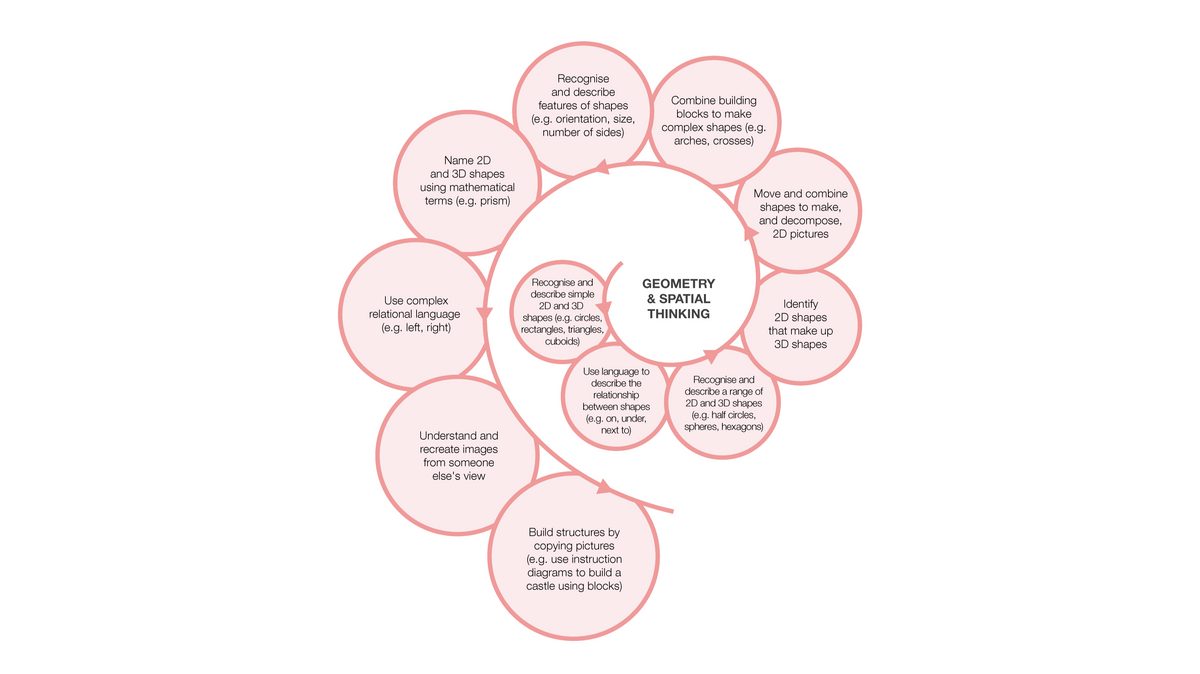
Approaches that educators can use to support the mathematical development of children include:
- teaching the association between number and quantity: supporting children to develop their familiarity with numbers and understanding of quantity in different ways, such as counting sets, subitising, and matching number words and symbols to quantity;
- promoting fluency with numbers and sequences: using a range of techniques including song and repetition to support children’s fluency with numbers (for example, numeral recognition) and sequences (such as the count sequence);
- teaching children problem-solving skills for maths: teaching and modelling problem-solving skills including effective ways to apply purposeful thinking;
- teaching and modelling how to make comparisons and connections: encouraging sorting collections into groups and promoting recognition of attributes that can also support with identifying and building patterns and sequences; and
- facilitating mathematical language: intentionally using specific, informal, and formal mathematical vocabulary in context to develop children’s understanding of concepts (receptive) and explain their ideas (expressive).
The page for each approach has two sections. The first is called ‘What does the evidence say?’ In this section, we share key messages about the approach from the research. The second section is called ‘Approach in action.’ This section provides practical examples of how the approach could be implemented in settings. It draws on the experience and expertise of educators.
Approach 5, Facilitating Mathematical Language, underpins the other four approaches. Educators use this approach for two purposes: (1) they support children to use and understand mathematical language and (2) they encourage children to apply their language skills to extend and show their mathematical thinking. The approach links closely with approaches for teaching communication and language (see Communication and Language). Please consider reviewing both sections of the Evidence Store when thinking about this approach.
Most studies underpinning the early mathematics approaches in the Evidence Store involved research with children aged four to six. A smaller number of studies involved research with children aged three or seven. Studies were included if the majority of children were aged six or under.
In addition to the evidence summaries, the Evidence Store also includes videos and written examples drawn from practice. These aim to be relevant across the early years age group. The Evidence Store provides a summary of evidence about what is likely to be beneficial based on existing evidence –‘best bets’ for what approaches might work. Your professional judgement and knowledge of the children is also needed to move from the information and examples to evidence-informed decisions about what could work best for the children in your setting.
The evidence also revealed broader strategies to improve children’s maths skills. These include:
- structuring maths learning;
- professional development for educators; and
- using education technology (EdTech).
Structuring maths learning
Evidence suggests that there are different ways to implement early mathematics approaches successfully. This means that early mathematics can be introduced into early years settings in different ways depending on how your setting operates. It can be effective to introduce a whole maths curriculum, supplemental activities – shorter activities that are in addition to usual activities, and integrating maths into everyday routines. However, the impact of maths activities varies from study to study. It is important for educators to monitor whether their strategy is working.
Evidence indicates that maths approaches are similarly effective in different group sizes, including in large groups, small groups, and one to –one., However, the latter two require more staff time. If delivering small group or individual sessions, educators may want to prioritise children at greater risk of not meeting expected levels of development.
Children’s mathematics skills can develop play as well as through more focused, explicit teachingFormal educator-directed approaches in which educators explicitly support children to develop specific ideas and skills.. Explicit teachingFormal educator-directed approaches in which educators explicitly support children to develop specific ideas and skills. is when educators explicitly support children to develop specific ideas and skills. Maths learning that combines explicit teachingFormal educator-directed approaches in which educators explicitly support children to develop specific ideas and skills. and play is likely to be beneficial. The evidence shows that embedding maths activities in daily routines throughout the day can also be effective.
The effectiveness of additional maths instruction (sometimes called ‘tutoring’) for young children is uncertain. There is a lack of evidence that focuses just on pre-schoolers. There is some indication that children supporting each other to learn maths (sometimes called ‘peer tutoring’) can be effective.
Professional development for educators
There is widespread consensus that both educators’ knowledge of mathematics and of how young children’s maths skills develop influences children’s early mathematical learning. However, there is a lack of research on professional development focuses on maths in the early years. More research would help to find out what is most effective for educators working in the early years sector and the children they work with. Until we know more about maths-specific professional development, the EEF’s guide to Effective Professional Development in the Early Years and accompanying systematic review may be helpful.
An example of an effective professional development programme for educators working in the early years is Maths Champions. Children aged three to four whose setting participated in the programme made an extra three months’ progress in maths compared to children who did not receive the programme. Children from lower income families made even greater progress.
Many of the studies underpinning the maths Evidence Store included an element of training for educators and found a positive effect on maths outcomes. Training for educators to deliver a specific set of activities or programme can be a part of introducing effective approaches to maths teaching in early years settings.
Education technology (EdTech)
‘EdTech’ encompasses many different approaches and devices, from robots to interactive apps and games. EdTech can have a positive impact on maths outcomes though more evidence is needed.
Some promising types of EdTech include:
- EdTech that teaches maths or provides opportunities to practice (for example, apps or computer-assisted instructionApps or computer-assisted instruction include computer- or tablet-based software. The software provides a controlled environment, such as a game. It often gives children feedback to help them learn as they go.); and
- EdTech that helps children to be aware of their own learning.
When EdTech is used, it works better if adults support children to use it. Not all kinds of EdTech have been researched with children in the early years. More research is needed to understand the impact of tools like calculators and robots. EdTech is a useful tool, but it is not always the most effective way to teach maths skills. Educators should monitor whether different uses of EdTech are working to support children’s maths learning in their setting.
EdTech can support the learning of children who are at greater risk of not meeting expected levels of development and children from lower income families. However, there is a risk that children who have more experience using technology will learn more from opportunities involving EdTech. When using EdTech, educators should make sure that all children are supported to access the learning.
The EEF’s Early Years and Key Stage 1 maths guidance report is focused on children aged three to seven. It draws largely on a review of the evidence on maths teaching for that age group (Hodgen et al, 2019). It focuses on broader areas where there is evidence that certain behaviours and activities can make a difference to children’s maths learning. This includes the importance of professional development, the need to dedicate time to mathematics teaching, and the value of targeted interventions when extra support is needed. This is different to the evidence store, which focuses specifically on approaches and practices that educators can use in face-to-face interactions with children using evidence from studies with children under six.